Best estimate codes have been recently introduced into safety evaluations for nuclear power plants, which use detailed models of complicated phenomena to realistically predict accident progression. As best estimate codes, system analysis codes consisting of models that simulate individual phenomena and equipment have been developed in various countries, such as TRACE in the United States [1]. In this study, a system analysis code AMAGI (Advanced Multi-fluid Analysis code for Generation of thermal-hydraulic Information) has been developed as a new program from its basic design, to reflect the latest technical knowledge and regulatory needs in the code and to be used in safety research and support for regulatory activities [2], [3].

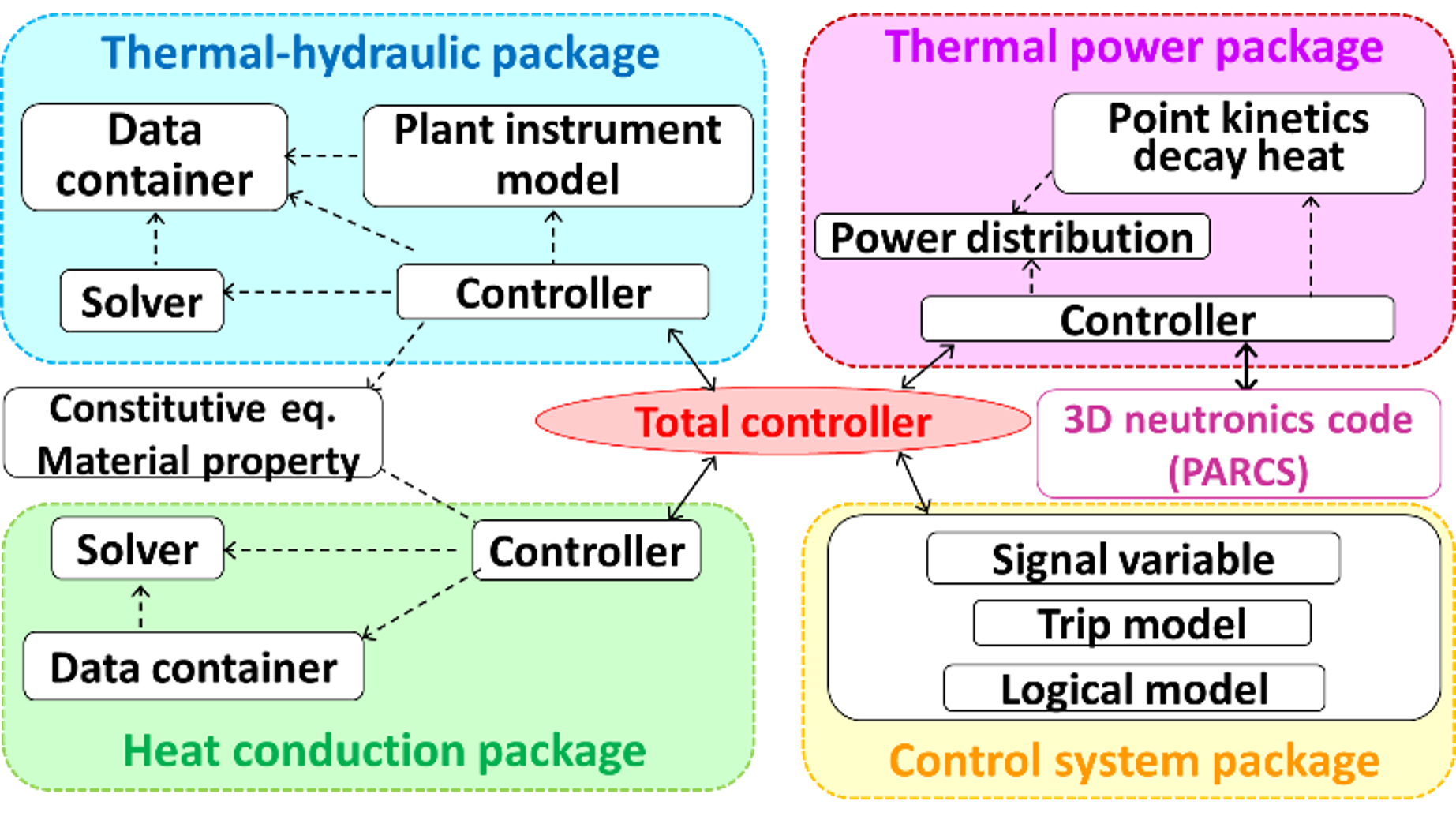
The analytical functions of AMAGI are based on the PIRT (Phenomena Identification and Ranking Table), where the phenomena that occur during representative events of the anticipated operation occurrences, design basis accidents and design extension conditions without significant fuel degradation in pressurized water reactors and boiling water reactors and their importance are identified [2]. They consist of thermal-hydraulic models, heat conduction models, control system models, and thermal power models. Figure 1 shows the system configuration of AMAGI [2]. The system consists of independent packages for each model so that each can be developed individually. A function in one package accesses those in other packages through the total controller. Therefore, AMAGI is a readable and extendable program for maintenance and future improvement. In the thermal-hydraulic model, conservation equations of mass, momentum and energy based on a two-fluid one-pressure model are solved with various constitutive equations used to simulate individual phenomena such as interface shear, wall shear, and wall heat transfer. In AMAGI, the same constitutive equations as in TRACE are used as the default model, and various constitutive equations based on the latest literature survey can be optionally used. In AMAGI, vapor generation from subcooled boiling is evaluated using Lahey's equation [4], as in TRACE. However, pumping factor is not considered in the evaluation in TRACE, while it is in AMAGI. To investigate the impact of the different constitutive equations, calculations using AMAGI were conducted for individual effect experiments on void fractions as part of the validation [3].

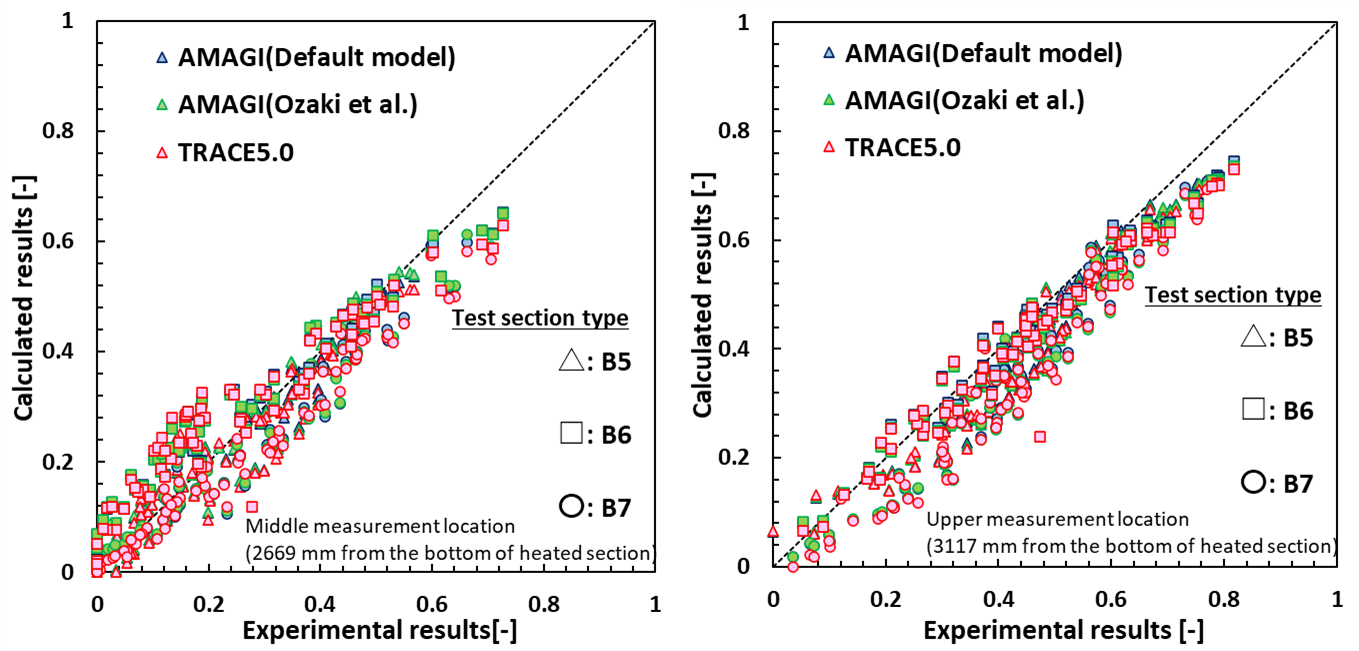
In the PSBT bundle steady-state void fraction experiments, steady-state void fractions in the central four subchannels at three different heights were measured under a wide range of conditions using 5 x 5 bundle test sections for gas-liquid two-phase flow in a PWR fuel assembly [5]. The measured void fraction is strongly influenced mainly by interfacial shear forces (e.g., bubble flow) and wall heat transfer (e.g., liquid single phase, subcooled boiling, nucleate boiling), and can be used to validate the analysis code for these phenomena. Figure 2 shows comparisons of experimental and calculated results for the void fraction measured in the middle and upper measurement locations [3]. In TRACE and AMAGI (Default model), the same constitutive equations are used for interfacial shear forces in the bubble flow to slag/churn flow regime. Constitutive equations such as equations of Ozaki et al. [6] are used in AMAGI (Ozaki et al.). At the middle measurement location, which is a shorter distance from the bottom of the heated section, there is a large difference between the analytical and the experimental results, especially for the experimental cases with low void fraction. Although the interface shear force models used in TRACE and AMAGI take accounts for their bubble distribution under subcooled boiling conditions, their predictive performance should be improved. On the other hand, the difference in results between the constitutive equation for interfacial shear force, which was additionally introduced into AMAGI, and the existing equation is small.

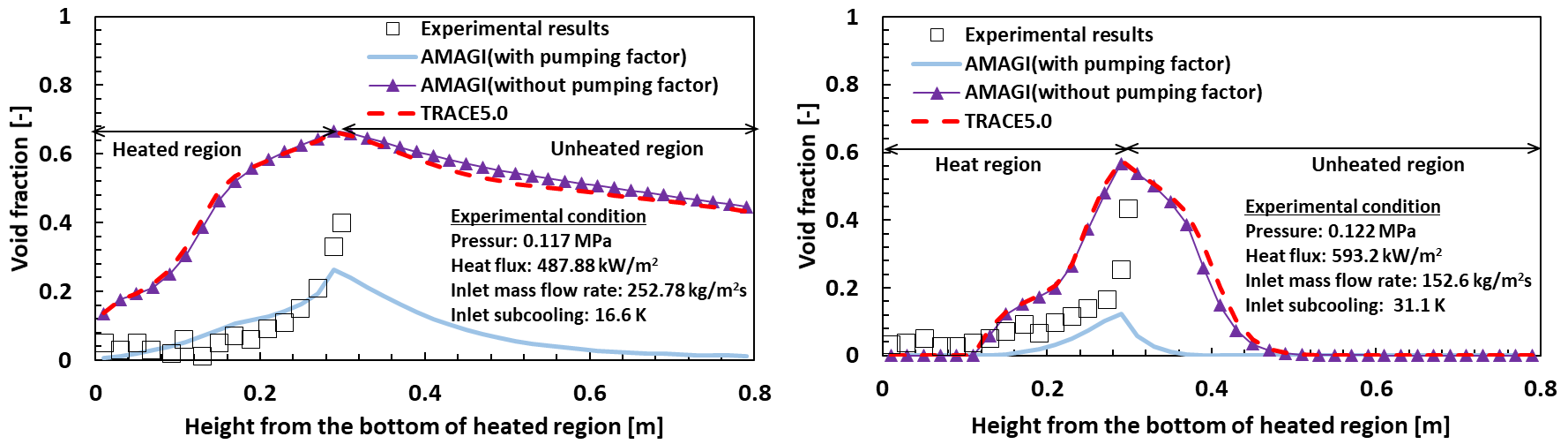
In the low-pressure subcooled void fraction experiments of Zeitoun et al., water at high subcooling was heated in an annular tube under atmospheric pressure conditions and the axial distribution of steady-state void fraction was measured [7]. The measured void fraction distribution can be used to validate the analysis codes for the onset of subcooled boiling and the void fraction increase under subcooled boiling, which are important in case of control rod drop accidents during cold shutdown. Figure 3 shows a comparison of the experimental and calculated results for the void fraction distribution in two experimental cases with different pressures, powers, etc. [3]. The calculated results without pumping factor (TRACE and AMAGI) and with pumping factor (AMAGI) show completely different axial void fraction distributions. In the calculations that do not consider the pumping factor, the increase in void fraction is significantly overestimated, but in the calculations with the pumping factor, the increase in void fraction is suppressed and qualitatively agrees with that in the experiments. However, the difference between the calculated and experimental results under atmospheric pressure conditions is still larger than that under high pressure conditions, and it is important to investigate further and improve the predictive performance of void fractions.

To validate AMAGI, various experiments were selected based on PIRT and calculations using AMAGI were conducted on the experiments, including the void fraction experiments described above. In the validation, technical knowledge was obtained on the differences between the AMAGI and TRACE models for each phenomenon and their impacts on the results of the analysis.

Click to open and enlarge.

References

[1] U.S. Nuclear Regulatory Commission, TRACE V5.0 THEORY MANUAL, Field Equation, Solution Methods, and Physical Models, U.S. Nuclear Regulatory Commission.

[2] J. Kaneko, N. Tsukamoto, Analytical Function and Development Status of the System Analysis Code for Nuclear Power Plants, Transactions of the Atomic Energy Society of Japan, 19(3), pp. 163–177, 2020 [in Japanese].

[3] N. Tsukamoto, J. Kaneko, M. Sekine, H. Ono, Y. Masuhara, H. Eguci, Study on best-estimate thermal-hydraulic evaluation for nuclear power plants, RREP-2023-2003, Secretariat of Nuclear Regulation Authority, May 2023, https://www.nra.go.jp/data/000434337.pdf [in Japanese].

[4] R.T. Lahey, F.J. Moody, The Thermal-Hydraulics of a Boiling Water Nuclear Reactor, American Nuclear Society, U.s, 1993.

[5] A. Rubin et al., OECD/NRC Benchmark based on NUPEC PWR Subchannel and Bundle Tests (PSBT), NEA/NSC/DOC(2010)1, 2010.

[6] T. Ozaki, T. Hibiki, Modeling of distribution parameter, void fraction covariance and relative velocity covariance for upward steam-water boiling flow in vertical rod bundle, Journal of Nuclear Science and Technology, 55, 386-399, 2018.

[7] O.M Zeitoun, Subcooled Flow Boiling Condensation, McMaster University, Ph.D Thesis, 1994.