Background

Over decades, advances in computing performance has been achieved through transistor miniaturisation, as predicted by Moore's law. Figure 1 illustrates 42 years evolution of Intel, AMD and IBM's microprocessors including transistor density, frequency, performance, power and number of cores. This graphic shows that although transistor count continues to increase, frequency has trapped out due to the current leakage phenomena defining the start of the multicore era. The multicore architectures are also reaching their limits due to the 'memory wall' imposed by the bandwidth of the channel between the CPU and memory subsystems associated with the traditional von Neumann computer architecture. Moreover, as transistors have shrunk, the industry is struggling to break through the “power wall” referring to the increase in the power density and the chip temperature.

Hence, the last few years have seen the emergence of non-von Neuman models designed to attain better trade-offs in terms of performance-cost-energy. Figure 2 illustrates two examples of such models. The first is based on configurable logic blocks (CLBs) used in Field Programmable Gate Arrays (FPGA) and the second one on memory resistors (memristors) used in Field Programmable Analogue Arrays (FPAA). Both architectures refer to approximate computing methods that could allow to save energy and computation costs via a trade off in terms of solution accuracy. This idea is motivated by the fact that very high precision of modern computing hardware might actually be excessive for many engineering applications where a much lower accuracy could in practice be sufficient. Moreover, for complex simulations, the solution accuracy will usually mainly be limited by e.g. physical modelling approximations, numerical discretization errors and/or various sources of uncertainties. Therefore, requirements in terms of computing precision could be relaxed such as to instead redirect the resources towards achieving e.g. higher spatial, energy or angular resolutions and/or to simply improve the statistics in simulations.

FPGA allows implementing low-precision arithmetics by the truncation of the precision in a floating-point number, allowing thereby for more arithmetic units and memory blocks on a chip. This approach has been successfully shown to reduce computational costs for several climate modelling and neural network related applications. That has motivated major hardware vendors to settle on mixed-precision hardware units to further enhance their performance.

FPAA takes advantage of the Kirchhoffs and Ohm's laws to perform matrix-vector multiplication. The chip contains multiple memristor crossbars. Each crossbar stores a matrix by changing the conductance values at the crossing points. The vector-matrix multiplication is then performed by supplying the input vector as voltage pulses to the rows and reading out the current outputs at the columns. The multiple crossbars can be adopted for a large matrix with sparse coefficients by slicing it into smaller matrices (active slices) of the same size. It has been shown recently that the memristor devices can be used to solve numerically partial differential equations for 2D domains.

The straightforward execution of a piece of code on approximate computing hardware likely will produce unacceptable results due to the solution quality loss or iteration divergence. Therefore, it is imperative to evaluate the performance of a numerical model at various precision levels before its deployment on specialised hardware. To fulfil this objective, we have designed a reactor core simulation environment tool called FEMCORE, which employs the Finite Element Method (FEM) for solving the reactor core equations in arbitrary arithmetic precisions. The new simulation environment has been integrated with the multi-precision analysis tools CADNA (Control of Accuracy and Debugging for Numerical Applications) and RPE (Reduced Precision Emulation).  

Multi-Precision Analysis

For numerical illustrations, we considered two elementary reactor core models: 1) point kinetics equations with lumped fuel and coolant temperatures; 2) a 1D two-group diffusion model. The point kinetic model was used for simulations of a hot zero power transient initiated by the insertion of reactivity. The diffusion model was used for analyses of the reactor eigenvalue problem. Overall, we found that traditional numerical algorithms exhibit reasonable tolerance with precision reduction as low as 17-23 bits. It holds true for both transient and eigenvalue problems, although we need to perform more tests to confirm this preliminary result. Another important observation is that in many cases, the precision was limited by the algorithm's convergence issue rather than degradation of solution accuracy.

Point Kinetics

The model is represented by a system of 9 ODEs: power P, six-group precursors C, lumped fuel and coolant temperatures Tf and Tc, and the linear model of temperature feedback. The equations have been integrated by a multi-step backward differentiation formula (BDF) method with a variable step size based on the Nordsik’s formulation and using the fixed-point iteration to resolve the in-step nonlinear system of equations. The linear system was resolved by a direct LU decomposition method that consumes most of the simulation run time.

Figure 3 shows the minimum floating-point arithmetic precision required to propagate the code’s input data without information loss. The precision is given in the number of significant digits for each entry of A matrix of the linear system A x = b solved by the LU method. The estimation was calculated by CADNA when simulated a 10-second power pulse caused by insertion of reactivity.

Figure 4 presents the rounding error for various floating-point arithmetic precisions as compared to the double precision. Note that the precision is given as number of bits for the significant part of a floating-point number; the highest number of bits is equal to 52 and refers to double floating-point arithmetic. Each point on the graph corresponds to specific coolant and fuel temperatures at the end of a 10-second transient. The rounding errors are compared to the uncertainties resulting from typical input data uncertainties for such transients. Thus, each grey point on the graphic represents the variation for a particular set of model’s input parameters. As indicated, the rounding error increases with a reduction in precision. More specifically, the uncertainty caused by a 11-bit truncation of the precision becomes comparable to uncertainties coming from input data.

Neutron Diffusion

The two-group diffusion eigenvalue equation was solved for an infinite slab geometry configuration with parameters taken from the ANL benchmark problem book. The solution method involves shift inverse power iterations and the inner linear system is solved using one of two methods:

• direct method based on the LU decomposition of a FEM matrix;
• iterative method using Gauss-Seidel to resolve the energy groups and BiCG solver to resolve the spatial variables.

The reduction of arithmetic precision was applied for the multiplication and division operations of the direct solution method and in the matrix-vector multiplication used by the iterative solution method.

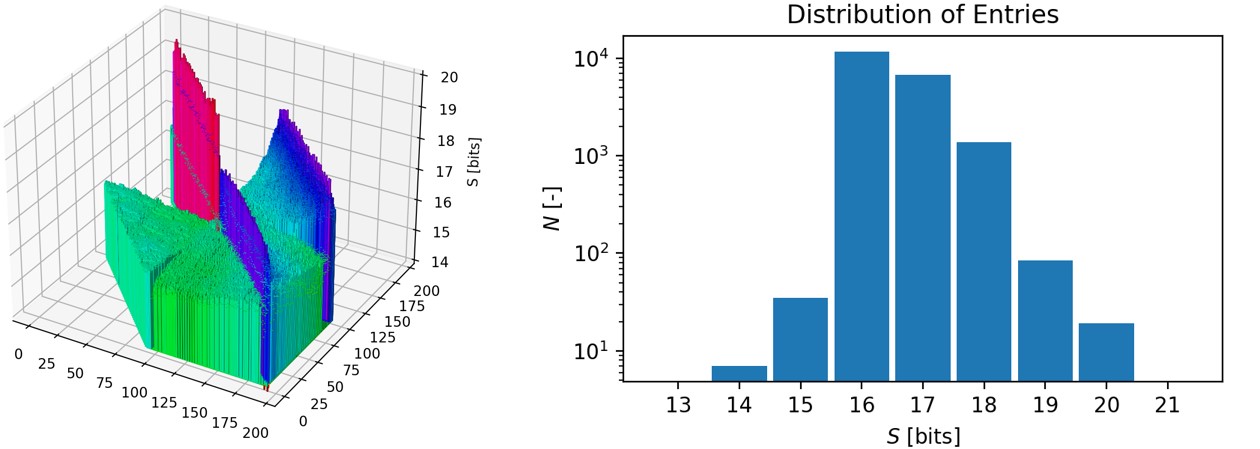
Figure 5 displays the distribution of significand’s bits over the entries of matrix A = LU estimated by the CADNA code assuming 0.1% uncertainty of input parameters. The number of bits is essentially non-uniform and varies in the range from 14 to 20 bits. Note that about a half of the LU matrix entries are permanently equal to zero due to the sparse structure of the input matrix A.

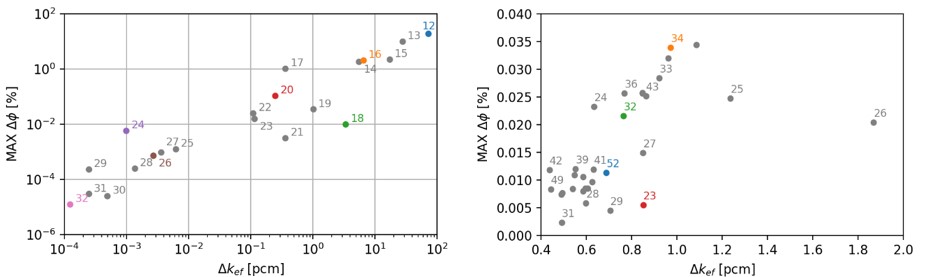
The reduction of arithmetic precision leads to a degradation of the solution accuracy. Figure 6 shows the rounding errors in neutron flux- and multiplication factor calculated by the direct LU and iterative GS/BiCG solvers. The accuracy of the iterative solver mostly depends on the given relative tolerance (RTOL) of the algorithm. Thus, the truncation of the floating-point numbers in the matrix-vector multiplication procedure causes fluctuations of the resulting solution around the reference within a given RTOL.

Future Work

Approximate computing can open immense resources for reactor core modelling and simulations. However, the robustness of traditional algorithms might become limited with regards to floating-point precision truncation and will in this case need to be adapted to the novel hardware. Therefore, our future work will be focused on multi-precision analysis of existing numerical algorithms to identify their performance and bottlenecks.